3nR
n-dimensional 3 in a Row
Rules for 4 players
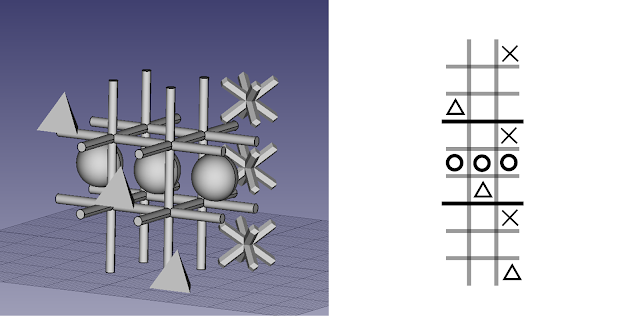
1. Each player has 3 pieces and you win when you place your pieces creating a “3nR”.
2. You have a “3nR” when your pieces are on any of the following dispositions:
· 3 pieces on a row inside a subboard (3x3 squares marked with bold lines)
· If you repeat the same position on 3 subboards on a row.
3. First all players place their pieces by turns on any empty box on the board. From the fourth round onwards each player moves one piece every round. You must move to an adjacent free box inside the subboard or to an adjacent subboard, on both cases the departure and arrival box must be contained inside a “3nR”.
3. First all players place their pieces by turns on any empty box on the board. From the fourth round onwards each player moves one piece every round. You must move to an adjacent free box inside the subboard or to an adjacent subboard, on both cases the departure and arrival box must be contained inside a “3nR”.
Rules for any number of players
The board is constructed joining 3 smaller boards. The rules stay the same, only now a subboard is any combination of boxes forming a smaller board.
The board is constructed joining 3 smaller boards. The rules stay the same, only now a subboard is any combination of boxes forming a smaller board.
Hypercubes
You probably have entered this place expecting a board game in n dimensions but you can only see flat boards (2D), that is because these boards are projections we use to picture objects of many dimensions on a piece of paper or on a screen. More precisely all our boards represent hypercubes and we play on as many dimensions as people are playing. In other words, 2 players play on a square, 3 players play on a cube, 4 players on a tesseract, 5 on a 5-cube, 6 on a 6-cube and so on. To properly understand how these projections represent these hyperdimensional objects we need to construct the boards from the very beginning.
Each board is constructed using 3 boards of an inferior dimension. Therefore we need to start with an object of zero dimensions, a point. The board that represents it is a single box. Then we move to one dimension, where we should have a segment. We represent this with three boxes forming a straight line. On two dimensions we can start building polygons; specifically we are looking for a square. If we place 3 1D boards side by side we have a 3x3 square, where we can start to play. On 3D we are looking for a cube and we should place 3 2D boards one on top of the other, creating a 3x3x3 cube. However, if we want to play on paper or on a screen we need a projection. The easiest way is to place the three floors side by side. That way we create the 9x3 board we see on the rules, with bold lines separating the different floors. A 4-cube, or tesseract, is the union of three cubes on a fourth dimension. If we use the projection we just have to place 3 boards for 3 players side by side. We can repeat this process up to any number of players, taking into account that the board grows exponentially.
If we play on the original cubes instead of the projections, all the 3nR are 3 adjacent pieces forming a straight line and all the allowed movements are adjacent boxes contained on a 3 in a Row.
If a game in higher dimensions is the kind of thing you find interesting then you must read the complete document. There we explore the mathematical properties of these hypercubes, we suggest new game mechanics to make this game even more interesting and in the last section we open a door to a mathematical world completly populated by incredible and surprising games. This document is on the download section together with boards and pieces, and more material about the game. And of course, everything here is completly open and free.
For more information: aivrobotics@gmail.com
Created and developed by: Adrián de la Iglesia Valls
Math and writing by: Adrián de la Iglesia and Jaime Mora Janicky
Graphics by: Adrián de la Iglesia Valls
Translation by: Adrián de la Iglesia and Pablo Emilio Jarillo Lobo
You probably have entered this place expecting a board game in n dimensions but you can only see flat boards (2D), that is because these boards are projections we use to picture objects of many dimensions on a piece of paper or on a screen. More precisely all our boards represent hypercubes and we play on as many dimensions as people are playing. In other words, 2 players play on a square, 3 players play on a cube, 4 players on a tesseract, 5 on a 5-cube, 6 on a 6-cube and so on. To properly understand how these projections represent these hyperdimensional objects we need to construct the boards from the very beginning.
Each board is constructed using 3 boards of an inferior dimension. Therefore we need to start with an object of zero dimensions, a point. The board that represents it is a single box. Then we move to one dimension, where we should have a segment. We represent this with three boxes forming a straight line. On two dimensions we can start building polygons; specifically we are looking for a square. If we place 3 1D boards side by side we have a 3x3 square, where we can start to play. On 3D we are looking for a cube and we should place 3 2D boards one on top of the other, creating a 3x3x3 cube. However, if we want to play on paper or on a screen we need a projection. The easiest way is to place the three floors side by side. That way we create the 9x3 board we see on the rules, with bold lines separating the different floors. A 4-cube, or tesseract, is the union of three cubes on a fourth dimension. If we use the projection we just have to place 3 boards for 3 players side by side. We can repeat this process up to any number of players, taking into account that the board grows exponentially.
If we play on the original cubes instead of the projections, all the 3nR are 3 adjacent pieces forming a straight line and all the allowed movements are adjacent boxes contained on a 3 in a Row.
Each board is constructed using 3 boards of an inferior dimension. Therefore we need to start with an object of zero dimensions, a point. The board that represents it is a single box. Then we move to one dimension, where we should have a segment. We represent this with three boxes forming a straight line. On two dimensions we can start building polygons; specifically we are looking for a square. If we place 3 1D boards side by side we have a 3x3 square, where we can start to play. On 3D we are looking for a cube and we should place 3 2D boards one on top of the other, creating a 3x3x3 cube. However, if we want to play on paper or on a screen we need a projection. The easiest way is to place the three floors side by side. That way we create the 9x3 board we see on the rules, with bold lines separating the different floors. A 4-cube, or tesseract, is the union of three cubes on a fourth dimension. If we use the projection we just have to place 3 boards for 3 players side by side. We can repeat this process up to any number of players, taking into account that the board grows exponentially.
If we play on the original cubes instead of the projections, all the 3nR are 3 adjacent pieces forming a straight line and all the allowed movements are adjacent boxes contained on a 3 in a Row.
If a game in higher dimensions is the kind of thing you find interesting then you must read the complete document. There we explore the mathematical properties of these hypercubes, we suggest new game mechanics to make this game even more interesting and in the last section we open a door to a mathematical world completly populated by incredible and surprising games. This document is on the download section together with boards and pieces, and more material about the game. And of course, everything here is completly open and free.
For more information: aivrobotics@gmail.com
Created and developed by: Adrián de la Iglesia Valls
Math and writing by: Adrián de la Iglesia and Jaime Mora Janicky
Graphics by: Adrián de la Iglesia Valls
Translation by: Adrián de la Iglesia and Pablo Emilio Jarillo Lobo